Low-rank Bayesian Tensor Factorization for Hyperspectral Image Denoising

Abstract

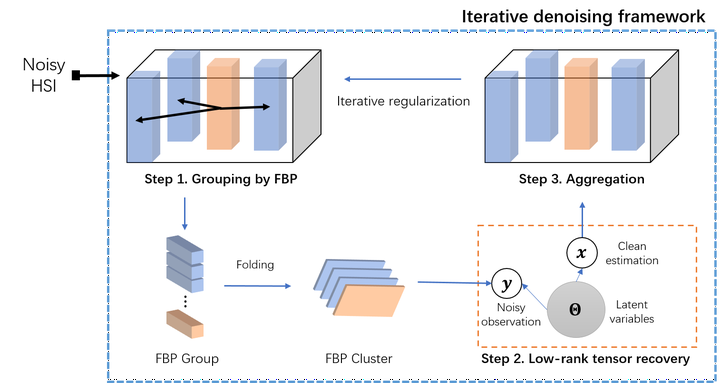
In this paper, we present a low-rank Bayesian tensor factorization approach for hyperspectral image (HSI) denoising problem, where zero-mean white and homogeneous Gaussian additive noise is removed from a given HSI. The approach is based on two intrinsic properties underlying a HSI, i.e., the global correlation along spectrum (GCS) and nonlocal self-similarity across space (NSS). We first adaptively construct the patch-based tensor representation for the HSI to extract the NSS knowledge while preserving the property of GCS. Then, we employ the low rank property in this representation to design a hierarchical probabilistic model based on Bayesian tensor factorization to capture the inherent spatial-spectral correlation of HSI, which can be effectively solved under the variational Bayesian framework. Furthermore, through incorporating these two procedures in an iterative manner, we build an effective HSI denoising model to recover HSI from its corruption. This leads to a state-of-the-art denoising performance, consistently surpassing recently published leading HSI denoising methods in terms of both comprehensive quantitative assessments and subjective visual quality.